[[[문제]]] 균등 분포와 정규 분포를 알아보자
[[[원리 분석]]]
uniform 분포
1. 구간과 횟수를 구하기 위해 map을 사용한다. key: 구간 value: 횟수
2. 예를들어 0 ~ 10000까지 숫자가 있다고 하면 0 ~ 999 = 구간 0, 1000 ~ 1999 = 구간 1
... 9000 ~ 9999 = 구간 9 이런식으로 구간을 나눈 뒤 횟수를 넣는다.
3. 각 구간에 얼마만큼 균일하게 값이 저장되었는지 파악할 수 있다.
4. 본문은 1 ~ 99999사이의 랜덤값을 백만번 만들고 구간을 1 ~ 9까지 만들어서 넣을 것이다.
그러니까 1 ~ 9999, 10000 ~ 19999 ... 90000 ~ 99999 구간을 총 9개 만든다.
9개 구간의 총 횟수는 백만개가 되야한다.
5. 디폴트 랜덤 엔진도 여러 비트를 이용하여 랜덤하게 만들기 때문에 강력하다.
==헤더 파일==
#include <iostream>
#include <map>
#include <random>
==전역 변수==
default_random_engine dre
uniform_int_distribution uid{ 1, 9'9999 }
==소스 코드==


꽤나 균등하다.
normal 분포
1. 평균과 분산을 이용한다.
2. 많은 자연 현상에서 발견할 수 있다.
3. 대부분의 데이터가 평균 주변에 모여있고 평균에서 멀어질수록 데이터의 빈도수가 적어진다.
4. 분산을 이용하여 고르게 분포하도록 만들 수 있다.
==헤더 파일==
#include <iostream>
#include <map>
#include <random>
==전역 변수==
default_random_engine dre
normal_distribution nd{99'999.}
==소스 코드==


대부분이 100'000에 뭉쳐있다.
==전역 변수==
default_random_engine dre
normal_distribution nd{ 5'0000. };
==소스 코드==

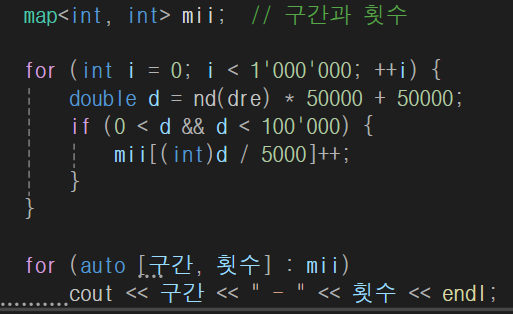
1. 정규분포에 평균을 50000으로 설정하였다.
2. 위의 정규 분포에 랜덤값 10000개를 만들었다.
3. 구간을 1만 단위로 나눈다.
4.d 를 0 ~ 99999까지 제한한 이유는 분산값을 균등하게 했을 때 0 ~ 99999까지의 수가 나올 수 있기 때문이다.
그 사실을 명확히 나타내기 위해 굳이 코드로 명시한 것임.
5. 근데 지금같은 경우는 대충 49998 ~ 50002 사이에 밀집해 있어서 암만 분산 값을 1에 가까이 한다고 해도
분산되지 않음.

결과: 대부분 5만 근처에 밀집해 있다.
노멀분포는 평균에 밀집해 있는 분포이기 때문이다.
normal 분포가 분산되게 해보자. 구간은 20개
normal_distribution nd{ 0.0 , 0.1 };
default_random_engine dre;
설명: 평균을 0으로 하고 0.1의 분산을 하면 야먀 -0.3 ~ 0.3 사이에 값이 분포될 것이다. ( 출처: chat gpt)
분산을 0.3으로 하면 거의 0.9 ~ 0.9 사이에 값이 분포되는걸로 확인함. 명확하진 않음.
정확히 얘기하자면 -0.3 ~ 0.3 사이에 있을 확률 몇퍼센트, -0.6 ~ 0.6 몇퍼센트 -0.9 ~0.9 몇퍼센트
이렇게 확률로 나와 있다.
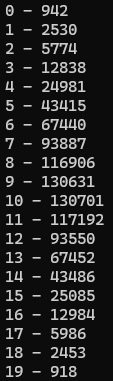
1. 총 합은 백만개가 되야 함
2. 위에서 말했듯 현재 -0.3 ~ 0.3 사이에 값이 분포됨.
따라서 * 50000 + 50000 하면 35000 ~ 65000사이에 값이 분포 됨
아래의 실행결과를 보자

구간을 20구간으로 나눴으니 25000 ~ 60000이라는 건데 위에서 예상한 값과 거의 근사하다.
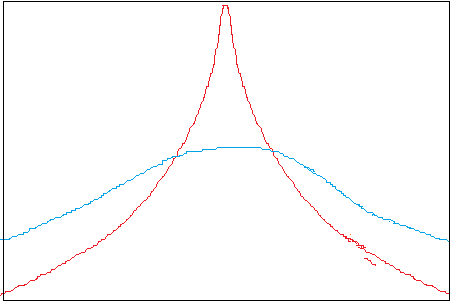
0.3으로 분포를 주면 대충 -0.6 ~ 0.6 이라 해도 매우 분산될거고 -0.9 ~ 0.9라 하면 더 분산될 것임.
0.9로 분산시켜보자

결론: 분산값이 1에 가까울수록 값이 고르게 분포된다.
이유는 평균이 0.0일 때 분산값이 1이면 -0.9999 ~ 0.9999 사이에서 값이 나올 것이다. -1 ~ 1은 안되는 듯 하다.
*50000 + 50000 했을 때 0 ~99999사이에서 고루 분포된다.
계산 방법
내가 그냥 생각한 거라 옳바르지 않을 수 있다. 평균을 0.0으로 잡았을 때 (최소 ~ 최대) = (-1 ~ 1)사이에서 값이 분포된다.
*50000 + 50000 했으니 0 ~ 100000사이에서 값이 분포되는데
분산 값이 0.0에 가까울 수록 평균인 50000 근처에 값이 몰리고 1에 가까울 수록 골고루 퍼진다.
축을 오른쪽으로 이동한 것이라고 봐도 된다.
학습 장소: 한국공학대학교 게임공학과 수업
참고: https://en.cppreference.com/w/
'---C++ 역량 강화--- > STL 공부' 카테고리의 다른 글
| high_resolution_clock (0) | 2024.05.29 |
|---|---|
| vector(+flat set), set, unordered set 찾기 속도 비교 (0) | 2024.05.28 |
| unordered_associative container 학습 (0) | 2024.05.28 |
| view adaptor (0) | 2024.05.27 |
| map 파일에 사용된 단어와 그 횟수를 출력하라. (0) | 2024.05.27 |